“浪潮杯”第九届山东省ACM大学生程序设计竞赛重现赛 B Bullet（二分+最大流）

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 65536K，其他语言131072K
64bit IO Format: %lld

题目描述

In GGO, a world dominated by gun and steel, players are fighting for the honor of being the strongest gunmen. Player Shino is a sniper, and her aimed shot kills one monster at a time. Now she is in an n*n map, and there are monsters in some grids. Each monster has an experience. As a master, however, Shino has a strange self-restrain. She would kill at most one monster in a column, and also at most one in a row. Now she wants to know how to get max experience, under the premise of killing as many monsters as possible.

输入描述

The first line contains an integer $n$.
$n<=500$
Then $n$ lines follow. In each line there are $n$integers, and $A_{ij}$ represents the experience of the monster at grid $(i,j)$.
If $A_{ij}=0$, there is no monster at grid $(i,j)$.
The experience is the minimal experience of all the monster which are killed.

It guaranteed that the maximum of the experience of the monster is not larger than $10^9$

输出描述

One integer, the value of max experience.

示例1

输入

2
2 0
1 8

输出

2

题目链接：B.Bullet

退役之后图论没怎么做了，只记得最短路了23333，实际是个简单题，很显然的网络流，考虑一行一列最多只能放一个，因此把行和列拿出来当做点，设源点为$S$，汇点为$T$，先把最低经验值设为$1$，跑一遍最大流得到最坏情况下的最多杀怪数，然后二分最小的经验值，每次选出大于等于当前假设经验值的怪物，重新建图跑最大流。

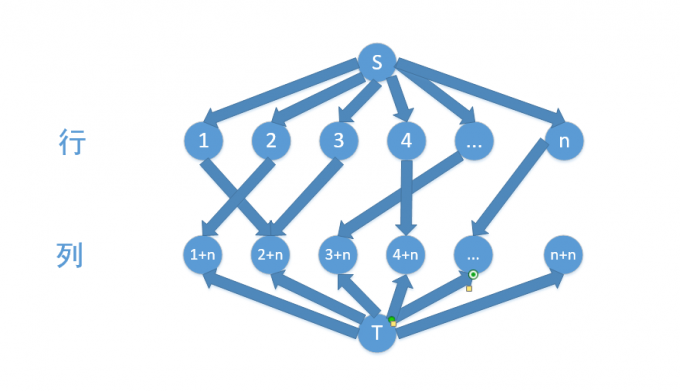
建图如下：

1. 对所有行建边：$(S,i,\infty)$
2. 对所有列建边：$(j+n,T,\infty)$
3. 如果位置$(i,j)$有怪物且其血量大于，则建边：$(i, n+j,1)$

代码：

#include <bits/stdc++.h>
//#pragma GCC optimize(2)
using namespace std;
#define INF 0x3f3f3f3f
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
#define pb(x) push_back(x)
#define sf(x) scanf("%d", &x)
#define all(a) (a).begin(),(a).end()
#define clr(arr,val) memset(arr,val,sizeof(arr))
#define FAST_IO ios::sync_with_stdio(false);cin.tie(0);
#define caseT int _T;scanf("%d",&_T);for (int q=1; q<=_T; ++q)
typedef pair<int, int> pii;
//typedef complex<double> cpx;
typedef long long ll;
const double PI = acos(-1.0);
const int N = 510;
struct edge
{
    int to, nxt, cap;
    edge() {}
    edge(int _to, int _nxt, int _cap): to(_to), nxt(_nxt), cap(_cap) {}
} E[(N * N + 2 * N) << 1];
int head[N << 1], tot, d[N << 1], G[N][N], n, S, T;

namespace sg {
    void init()
    {
        clr(head, -1);
        tot = 0;
    }
    inline void add(int s, int t, int cap)
    {
        E[tot] = edge(t, head[s], cap);
        head[s] = tot++;
        E[tot] = edge(s, head[t], 0);
        head[t] = tot++;
    }
    int bfs(int s, int t)
    {
        clr(d, -1);
        d[s] = 0;
        queue<int>Q;
        Q.push(s);
        while (!Q.empty())
        {
            int u = Q.front();
            Q.pop();
            for (int i = head[u]; ~i; i = E[i].nxt)
            {
                int v = E[i].to;
                if (d[v] == -1 && E[i].cap > 0)
                {
                    d[v] = d[u] + 1;
                    if (v == t)
                        return 1;
                    Q.push(v);
                }
            }
        }
        return ~d[t];
    }
    int dfs(int s, int t, int f)
    {
        if (s == t || !f)
            return f;
        int ret = 0;
        for (int i = head[s]; ~i; i = E[i].nxt)
        {
            int v = E[i].to;
            if (d[v] == d[s] + 1 && E[i].cap > 0)
            {
                int df = dfs(v, t, min(f, E[i].cap));
                if (df > 0)
                {
                    E[i].cap -= df;
                    E[i ^ 1].cap += df;
                    ret += df;
                    f -= df;
                    if (!f)
                        break;
                }
            }
        }
        if (!ret)
            d[s] = -1;
        return ret;
    }
    int dinic(int s, int t)
    {
        int ret = 0;
        while (bfs(s, t))
            ret += dfs(s, t, INF);
        return ret;
    }
}
inline int calc(int k)
{
    sg::init();
    for (int i = 1; i <= n; ++i)
    {
        sg::add(S, i, 1);
        for (int j = 1; j <= n; ++j)
        {
            if (G[i][j] >= k)
                sg::add(i, j + n, 1);
        }
        sg::add(i + n, T, 1);
    }
    return sg::dinic(S, T);
}
int main(void)
{
    int i, j;
    int l = 0, r = 0;
    sf(n);
    for (i = 1; i <= n; ++i)
        for (j = 1; j <= n; ++j)
            sf(G[i][j]), r = max(r, G[i][j]);
    S = 0, T = n << 1 | 1;
    int b = calc(1), ans = 0;
    while (l <= r)
    {
        int mid = MID(l, r);
        if (calc(mid) < b)
            r = mid - 1;
        else
        {
            l = mid + 1;
            ans = mid;
        }
    }
    printf("%d\n", ans);
    return 0;
}